| (%i1) | load("/home/vcaeken/Desktop/rfMaxima.mac")$ |

Capacitive Fixed-Fixed Beam RF MEMS SPST Switch
(See "RF MEMS Theory, Design and Technology", by G. M. Rebeiz, Wiley, 2003)
1 Model Parameters
1.1 Dimensions
g_0: nominal gap height [m^2]
l: beam length [m]
t: beam thickness [m]
t_d: dielectric thickness [m]
w: beam width [m]
W: electrode width [m]
| (%i2) |
g_0:2e-6$ l:300e-6$ t:0.5e-6$ t_d:0.2e-6$ w:80e-6$ W:100e-6$ |
A: electrode area [m^2]
| (%i8) | A:W*w; |

1.2 Material Parameters
Beam (Al, Au, Cu, UNCD):
%nu: Poisson ratio of the beam material []. The Poisson ratio of Au is 0.44.
%rho: mass density of the beam material [kg/m^3]. The mass density of Au is 19200 kg/m^3.
%sigma: residual stress of the beam material [Pa]. Assume 20 to 160 MPa.
E: Young's modulus of the beam material [Pa]. The Young's modulus of Au is 78 GPa.
Dielectric (silicon dioxide, silicon nitride):
%epsilon_0: permittivity of vacuum [F/m]
%epsilon_r: dielectric's dielectric constant []. The dielectric constant of Si_3N_4 is 6-9.
Gas (air, nitrogen):
%lambda: mean-free path, distance covered by a molecule in a gas between successive collisions [m]
%mu: viscosity coefficient, measure of resistance of a gas to changes in the transport of molecular momentum [kg/(m.s)]
| (%i9) |
%rho:19.2e3$ E:78e9$ %nu:0.44$ %sigma:100e6$ %epsilon_0:8.854e-12$ %epsilon_r:7.6$ %lambda:1.5e-7$ %mu:1.845e-5$ |
2 Electromechanical Properties & Figures of Merit
2.1 Static Properties & Figures of Merit
m: effective beam mass [kg]
k: distributed force spring constant, incl. residual stress [N/m]
k_s: stretching coefficient [N/m^3]
V_p: pull-in voltage [V]
V_bias: bias voltage [V]
f_m_0: mechanical resonant frequency [Hz]
Q_m: mechanical quality factor []
b: damping coefficient [N.s/m]
H(%i*%omega):=X(%i*%omega)/F(%i*%omega), mechanical transfer function [m/N]
| (%i17) |
m:0.4*%rho*l*t*w; k_1:(32*E*t^3*w)/l^3*(27/49); k_2:(8*t*w*(1-%nu)*%sigma)/l*(3/5); k:k_1+k_2; k_s:float((t*w*%pi^4*E)/(64*l^3)); V_p:sqrt((8*k*(g_0+t_d/%epsilon_r)^3)/(27*A*%epsilon_0)); V_bias:40; t_s:3.67*V_p/(V_bias*sqrt(k/m)); f_m_0:float(sqrt(k/m)/(2*%pi)); Q_m:sqrt(k/k_1)*(sqrt(E*%rho)*t^2*g_0^3)/(%mu*(w*l/2)^2); b:k/(2*%pi*f_m_0*Q_m); H(f):=1/(k*(1-(f/f_m_0)^2+%i*(f/(Q_m*f_m_0)))); |

| (%i29) |
wxplot2d([ev(20*log10(abs(H(f))))], [f,1,1e7], [logx], [legend,false], [xlabel,"Frequency [Hz]"], [ylabel,"20*log10(Abs(H(f)))"], [style,[lines,3,11]], [gnuplot_preamble,"set grid"])$ |
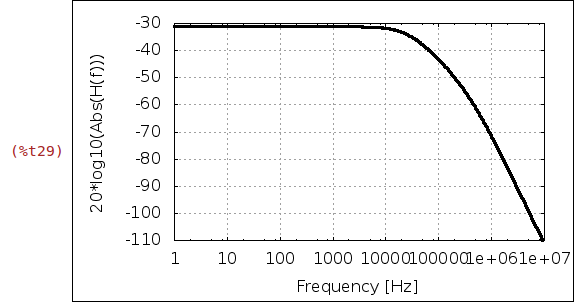
2.2 Dynamic Properties & Figures of Merit
| (%i30) | kill(t); |
Q_m: variable mechanical quality factor []
b: variable damping coefficient [N.s/m]
| (%i31) | Q_m(z):=Q_m*(1+9.9638*(%lambda/(g_0-z))^1.159)*(1-(z/g_0)^2)^(3/2); |

| (%i32) | b(z):=k/(2*%pi*f_0*Q_m(z)); |

F_e: electrostatic force [N]
| (%i33) | F_e(z,t):=(%epsilon_0*A*(V_C)^2)/(2)*(1/(g_0+t_d/%epsilon_r-z)^2); |
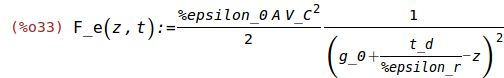
F_VdW: Van der Waals forces [N]
| (%i34) |
c_1:10e-80; c_2:10e-75; |

| (%i36) | F_VdW(z):=c_1*A/(g_0-z)^3-c_2*A/(g_0-z)^10; |

Maxima's ordinary differential equation (ODE) solver ode2 solves elementary linear ODEs
of first and second order. The function contrib_ode extends ode2 with additional methods
for linear and non-linear first order ODEs and linear homogeneous second order ODEs. The
code is still under development and the calling sequence may change in future releases.
Once the code has stabilized it may be moved from the contrib directory and integrated
into Maxima.
| (%i37) | load('contrib_ode)$ |

| (%i38) | contrib_ode(m*'diff('diff(z(t),t),t)=-k/(2*%pi*f_m_0*Q_m)*'diff(z(t),t)-k*z(t)+F_e(z(t),t),z,t); |
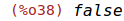
3 RF Properties & Figures of Merit
3.1 Small Signal Properties & Figures of Merit
C_u: up-state capacitance [F]
C_d: down-state capacitance [F]
f: RF frequency [GHz]
R_s: RF beam resistance [Ohm]
| (%i39) |
C_u:1.4*%epsilon_0*A/(g_0+t_d/%epsilon_r); C_d:0.65*%epsilon_0*A/(t_d/%epsilon_r); f:10e9$ R_s:1; |

C_r: capacitance ratio []
Q: RF quality factor []
| (%i43) |
C_r:C_d/C_u; Q:float(1/(2*%pi*f*R_s*C_u)); |
