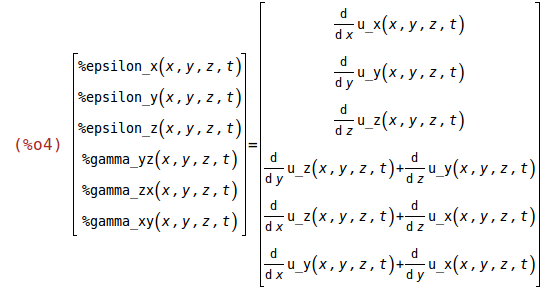
Appendix 2: Film Bulk Acoustic Resonator (FBAR)

(See: Microsystem Design by Stephen D. Senturia, pp. 192-193, 570-577)
(See: An Introduction to the Theory of Piezoelectricity by Jiashi Yang, pp. 89-93)

1 Linear Piezoelectricity

1.1 Displacement (u), Strain (S), and Stress (T)

u: displacement [m]

(%i1) u:matrix([u_x(x,y,z,t)],[u_y(x,y,z,t)],[u_z(x,y,z,t)])$
u2S(u):=matrix([diff(u[1,1],x)],[diff(u[2,1],y)],[diff(u[3,1],z)],[diff(u[2,1],z)+diff(u[3,1],y)],[diff(u[1,1],z)+diff(u[3,1],x)],[diff(u[1,1],y)+diff(u[2,1],x)])$

S: strain [] (%epsilon: normal strain, %gamma: shear strain)

(%i3) S:matrix([%epsilon_x(x,y,z,t)],[%epsilon_y(x,y,z,t)],[%epsilon_z(x,y,z,t)],[%gamma_yz(x,y,z,t)],[%gamma_zx(x,y,z,t)],[%gamma_xy(x,y,z,t)])$
S=u2S(u);

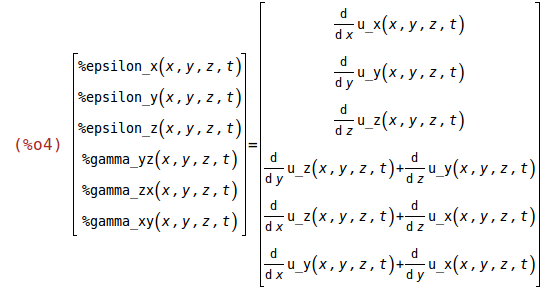
(%i5) grad(u):=matrix([diff(u[1,1],x,1),diff(u[1,1],y,1),diff(u[1,1],z,1)],[diff(u[2,1],x,1),diff(u[2,1],y,1),diff(u[2,1],z,1)],[diff(u[3,1],x,1),diff(u[3,1],y,1),diff(u[3,1],z,1)])$
grad(u);
1/2*(grad(u)+transpose(grad(u)));

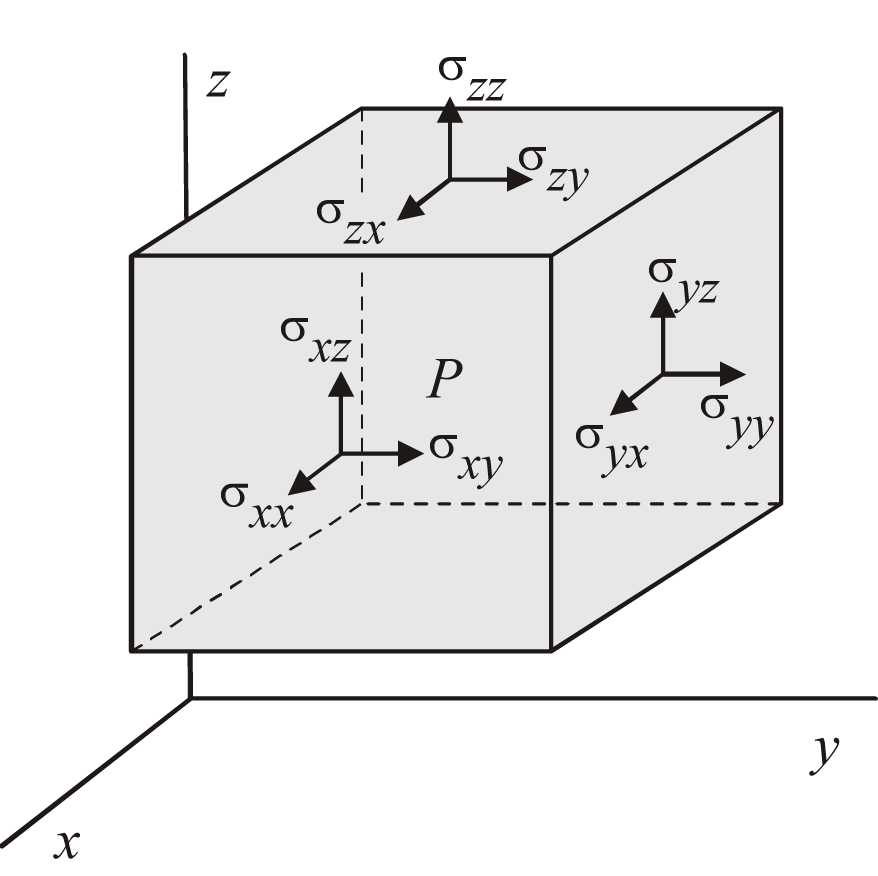
T: stress, force per unit area [N/m^2] (%sigma: normall stress, %tau: shear stress)

(%i8) T:matrix([%sigma_x(x,y,z,t)],[%sigma_y(x,y,z,t)],[%sigma_z(x,y,z,t)],[%tau_yz(x,y,z,t)],[%tau_zx(x,y,z,t)],[%tau_xy(x,y,z,t)]);
divT(T):=matrix([diff(T[1,1],x,1)+diff(T[6,1],y,1)+diff(T[5,1],z,1)],[diff(T[6,1],x,1)+diff(T[2,1],y,1)+diff(T[4,1],z,1)],[diff(T[5,1],x,1)+diff(T[4,1],y,1)+diff(T[3,1],z,1)])$
divT(T);

1.2 Electric Displacement (D) and Electric Field (E)

D: electric displacement [C/m^2]

(%i11) D:matrix([D_x(x,y,z,t)],[D_y(x,y,z,t)],[D_z(x,y,z,t)]);
divD(D):=matrix([diff(D[1,1],x,1)],[diff(D[2,1],y,1)],[diff(D[3,1],z,1)])$
divD(D);

E: electric field [V/m]

(%i14) E:matrix([E_x(x,y,z,t)],[E_y(x,y,z,t)],[E_z(x,y,z,t)]);

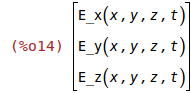
1.3 Linear Constitutive Tensors

The number of independent non-zero constants depends on the crystal symmetry. AlN and ZnO are materials of the 6mm crystal class.

%epsilon: dielectric permittivity tensor [C/(V.m)] (at constant strain)

(%i15) declare([%epsilon_0,%epsilon_11,%epsilon_33],[constant,real,scalar])$
%epsilon:matrix([%epsilon_11,0,0],[0,%epsilon_11,0],[0,0,%epsilon_33]);

C: elastic stiffness tensor [N/m^2] (at constant electric field)

(%i17) declare([C_11,C_12,C_13,C_33,C_44],[constant,real,scalar])$
C:matrix([C_11, C_12, C_13, 0, 0, 0],[C_12, C_11, C_13, 0, 0, 0],[C_13, C_13, C_33, 0, 0, 0],[0, 0, 0, C_44, 0, 0],[0, 0, 0, 0, C_44, 0],[0, 0, 0, 0, 0, (C_11-C_12)/2]);

e: piezoelectricity tensor [C/m^2]

(%i19) declare([e_15,e_31,e_33],[constant,real,scalar])$
e:matrix([0,0,0,0,e_15,0],[0,0,0,e_15,0,0],[e_31,e_31,e_33,0,0,0]);

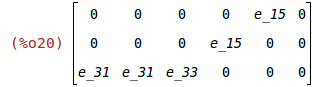
1.4 Lippmann's Linear Constitutive Equations in Charge-Stress Form

(%i21) T:C.S-transpose(e).E;
D:e.S+transpose(%epsilon).E;

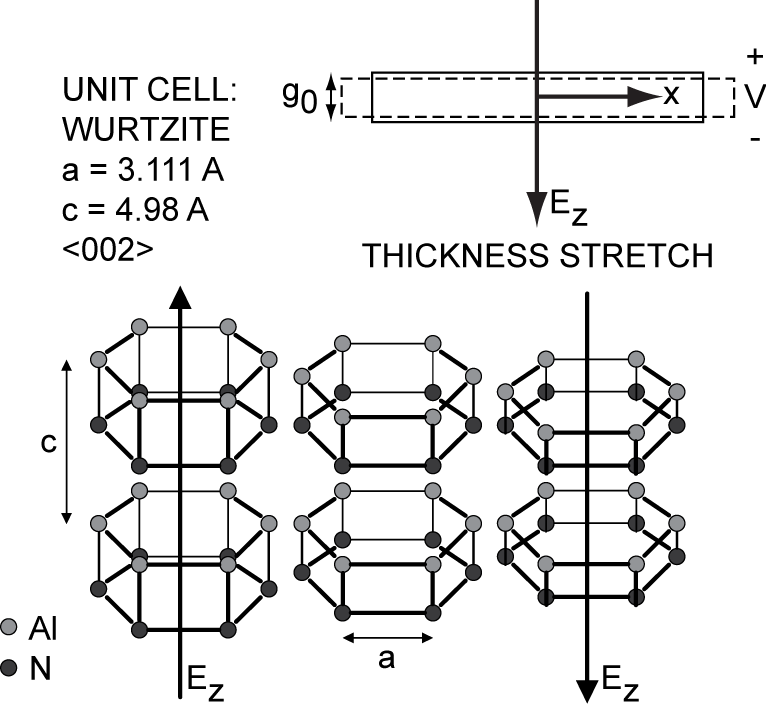
2 Boundary Value Problem

Assume a thickness-stretch vibration of an AlN plate, excited by an electric field along the Z-axis.
Assume the plate can not move along the X- and Y-axis: u_x(z,t)=0, u_y(z,t)=0.

(%i23) %epsilon_x(x,y,z,t):=0$
%epsilon_y(x,y,z,t):=0$
%epsilon_z(x,y,z,t):=diff(u_z(z,t),z,1)$
%gamma_yz(x,y,z,t):=0$
%gamma_zx(x,y,z,t):=0$
%gamma_xy(x,y,z,t):=0$

Assume the X- and Y-component of the electric field to be zero: E_x(x,y,z,t)=0, E_y(x,y,z,t)=0.

(%i29) E:matrix([0],[0],[E_z(z,t)]);
T:ev(C.S-transpose(e).E);
D:ev(e.S+transpose(%epsilon).E);

2.1 Potential Energy

Electrostatic Energy Density, w_e

(%i32) w_e:expand(ev(1/2*transpose(E).D));

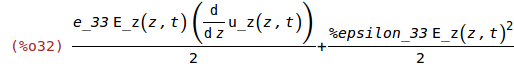
Elastic Energy Density, w_m

(%i33) w_m:expand(ev(1/2*transpose(S).C.S));

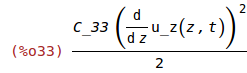
Total Energy Density

(%i34) w_t:w_e+w_m;

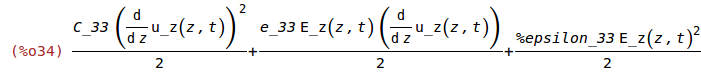
2.2 Newton's Law of Motion for a Continuum [PDE in AlN Volume]

Force density

(%i35) ev(T);
f:ratsimp(divT(ev(T)));

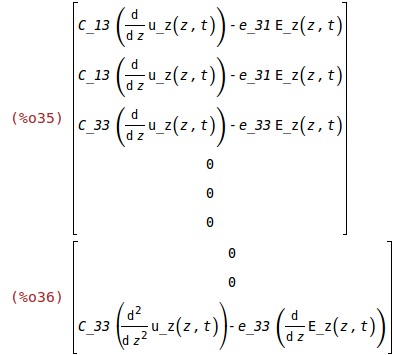
Viscosity and Q Factor

%eta: viscosity tensor [N/(m^2.s)]
%tau_m is the motional time constant
%omega_m is the mechanical resonant radian frequency
Q_m is the mechanical Q factor

(%i37) %tau_m:1/(%omega_m*Q_m);
%eta:%tau_m*C;

Newton's Law of Motion for a Continuum

%rho: mass density [kg/m^3]

(%i39) f=%rho*diff(u,t,2);

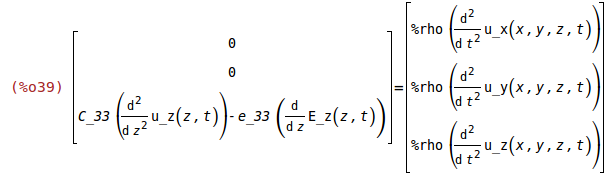
(%i40) f_z:ev(f[3,1]);
f_z=%rho*diff(u_z(z,t),t,2);

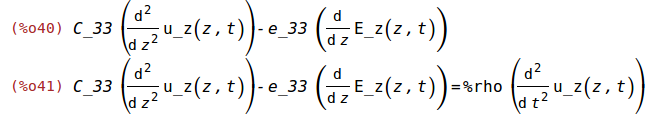
3 Gauss' Law [PDE in AlN Volume]

(%i42) divD(ev(D))=matrix([0],[0],[0]);

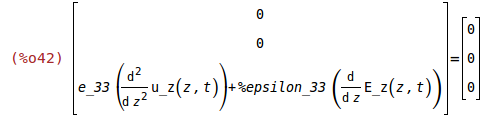
Calculating 'diff(E_z(z,t),z,1)

(%i43) -e_33*(diff(u_z(z,t),z,2))/%epsilon_33;

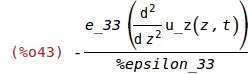
Calculating E_z(z,t)
B_1 is an integration constant.

(%i44) declare([B_1],[constant,real,scalar])$
define(E_z(z,t),-(e_33*(diff(u_z(z,t),z,1)))/%epsilon_33-B_1);

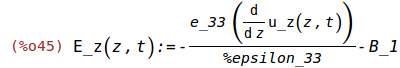
4 Boundary Conditions at the Plate Surface

Assume a solution u_z(z,t):=A_1*sin(%xi*z)*exp(%i*%omega_m*t) with %xi:sqrt(%rho/(C_33*(1+k_33^2)))*%omega
k_33: sqrt(e_33^2/(%epsilon_33*C_33))

(%i46) declare([A_1],[constant,real,scalar])$
u_z(z):=A_1*sin(%xi*z);
ratsimp(diff(u_z(z),z,1));
ratsimp(diff(u_z(z),z,2));

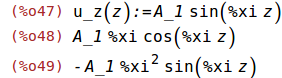
(%i50) define(T_z(z),C_33*(1+k_33^2)*%th(2)+e_33*B_1);
D_z(z):=-%epsilon_33*B_1;
define(E_z(z),-(e_33*%th(4))/%epsilon_33-B_1);
define(f_z(z),C_33*(1+k_33^2)*%th(4));
define(f_s_z(z),C_33*%th(5));
define(f_p_z(z),-e_33*(diff(E_z(z),z,1)));

Calculating the potential %Phi(z)
B_2 is an integration constant.

(%i56) declare([B_2],[constant,real,scalar])$
%Phi(z):=e_33*u_z(z)/%epsilon_33+B_1*z+B_2;

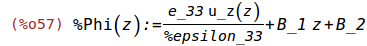
%sigma_z(z=-g_0/2)=0,
%sigma_z(z=g_0/2)=0,
%Phi(z=g_0/2)-%Phi(z=-g_0/2)=V
with,
g_0: thickness [m]
V: applied voltage [V]

(%i58) solve([ev(T_z(g_0/2))=0,ev(%Phi(g_0/2)-%Phi(-g_0/2))=V],[A_1,B_1])$
A_1:ratsimp(ev(A_1,%));
B_1:ratsimp(ev(B_1,%th(2)));
ratsimp(ev(A_1,%xi=%pi/g_0));
ratsimp(ev(B_1,%xi=%pi/g_0));

5 Elastic Wave Equation and Christoffel Equation

(See: http://sepwww.stanford.edu/public/docs/sep92/hector1/paper_html/node2.html)

(%i63) K:ev(1/k*matrix([k_x,0,0,0,k_z,k_y],[0,k_y,0,k_z,0,k_x],[0,0,k_z,k_y,k_x,0]),k_x=0,k_y=0);
k:ev(sqrt(k_x^2+k_y^2+k_z^2),k_x=0,k_y=0);

(%i65) M:ratsimp(k^2/%rho*K.subst(C_33*(1+k_33^2),C_33,C).transpose(K));
ratsimp(eigenvalues(M));
ratsimp(eigenvectors(M));

The BAW vibration frequency, f_m, can be used to determine the thickness of the AlN plate, g_0

(%i68) declare([%rho,C_33,g_0,k_33],[constant,real,scalar])$
assume(%rho>0)$
assume(C_33>0)$
assume(g_0>0)$
assume(k_33>0)$
k_z:2*%pi/(2*g_0);
%omega_m:sqrt(ev((k_z^2*C_33*(1+k_33^2))/(%rho)));
f_m:1/(2*%pi)*%omega_m;

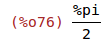
(%i76) ratsimp(sqrt(%rho/(C_33*(1+k_33^2)))*%omega_m*g_0/2);

m is the effective mass.
A is the electrode area.

(%i77) declare([A],[constant,real,scalar])$
m:A*integrate(u_z(z)^2*%rho,z,0,g_0/2)/A_1^2$
m:ev(m,%xi=sqrt(%rho/(C_33*(1+k_33^2)))*%omega_m);

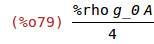
k_1_eff is the effective linear spring constant.

(%i80) solve([%omega_m=sqrt(k_1_eff/m)],[k_1_eff])$
k_1_eff:ev(k_1_eff,%);

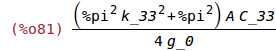
Tf is the linear temperature coefficient of frequency.

(%i82) Tf:'diff(log(f_m),Temp);

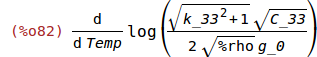
6 Charge, q, on the Electrodes

(%i83) q:ratsimp(-D_z(g_0/2)*A);

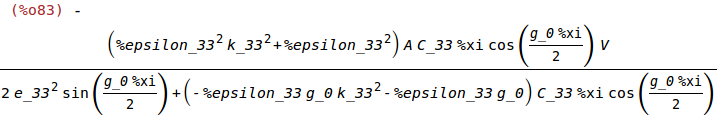
7 Motional Capacitance, C_m, Static Capacitance, C_0, and Transduction Factor, %eta

(%i84) C_FBAR:ev(q/V,
    %xi=sqrt(%rho/(C_33*(1+e_33^2/(%epsilon_33*C_33))))*%omega,
    k_33=sqrt(e_33^2/(%epsilon_33*C_33)));
C_0:ratsimp(limit(C_FBAR,%omega,0));
ratsimp(C_FBAR-C_0)$
C_m:ratsimp(ev(k_33^2*C_0,
    k_33=sqrt(e_33^2/(%epsilon_33*C_33))));
%eta:ratsimp(sqrt(k_33^2*k_1_eff*%epsilon_33*A/g_0*(1+k_33^2)));

8 Material Parameters

8.1 Hexagonal Aluminum Nitride (Wurtzite, Crystal Class 6mm)

(See "Material Parameters of AlN and LiAlO2 Single Crystals", by A. V. Sotnikov, H. Schmidt, M. Weihnacht, E. P. Smirnova, T. Yu. Chemekova, Yu. N. Makarov, IEEE IFCS, pp. 935-938, 2009)

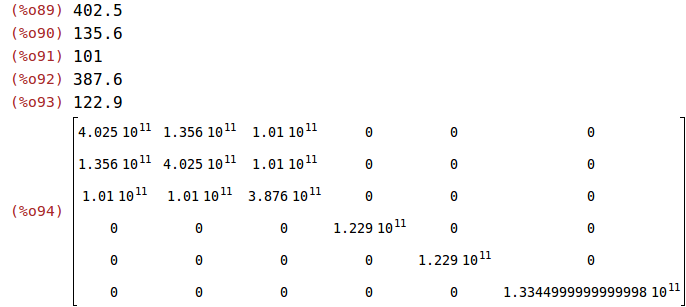
(%i89) C_11:402.5;
C_12:135.6;
C_13:101;
C_33:387.6;
C_44:122.9;
C:1e9*matrix([C_11, C_12, C_13, 0, 0, 0],[C_12, C_11, C_13, 0, 0, 0],[C_13, C_13, C_33, 0, 0, 0],[0, 0, 0, C_44, 0, 0],[0, 0, 0, 0, C_44, 0],[0, 0, 0, 0, 0, (C_11-C_12)/2]);

(%i95) e_33:1.34;
e_31:-0.6;
e_15:-0.32;
e:matrix([0,0,0,0,e_15,0],[0,0,0,e_15,0,0],[e_31,e_31,e_33,0,0,0]);

(%i99) %epsilon_0:8.854e-12;
%epsilon_11:9;
%epsilon_33:9.5;
%epsilon:%epsilon_0*matrix([%epsilon_11,0,0],[0,%epsilon_11,0],[0,0,%epsilon_33]);

(%i103) %rho:3260;