(%i1) load("/home/vcaeken/Desktop/rfMaxima.mac")$

2nd Order Butterworth Filter,
Implemented Using Sallen–Key Topology

(see http://en.wikipedia.org/wiki/Butterworth_filter)

1 Filter Design

(%i2) declare([C_1,C_2,R_1,R_2,%omega_b,%omega_c],[constant,real,scalar])$
assume(C_1>0)$
assume(C_2>0)$
assume(R_1>0)$
assume(R_2>0)$
assume(%omega_b>0)$
assume(%omega_c>0)$

(%i9) G(s):=1/(1+C_2*(R_1+R_2)*s+C_1*C_2*R_1*R_2*s^2);
expand(ev(abs(denom(G(s)))^2,s=%i*%omega));

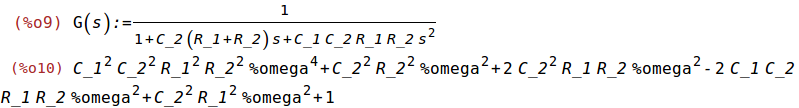
(%i11) solve([%omega_c^4=1/(C_1^2*C_2^2*R_1^2*R_2^2),C_2^2*R_2^2+2*C_2^2*R_1*R_2-2*C_1*C_2*R_1*R_2+C_2^2*R_1^2=0],[C_1,C_2,R_1,R_2]);

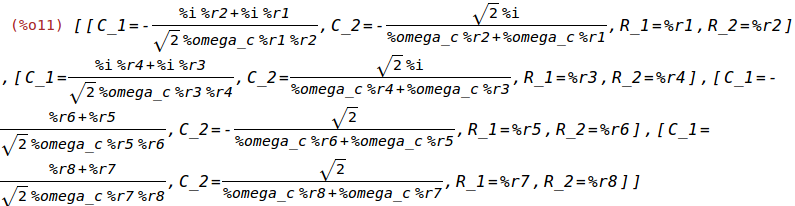
We have two degrees of freedom to realize the 2nd order Butterworth filter, given
%omega_c. Let us therefore assume R_1=1000 Ohm and R_2=1000 Ohm.

(%i12) Butterworth:ev([C_1=(%r8+%r7)/(sqrt(2)*%omega_c*%r7*%r8),C_2=sqrt(2)/(%omega_c*%r8+%omega_c*%r7),R_1=%r7,R_2=%r8],%r7=1000,%r8=1000);

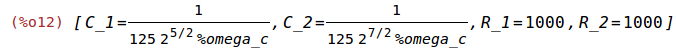
(%i13) define(G_REALIZED(s),ratsimp(ev(G(s),C_1=ev(C_1,Butterworth),C_2=ev(C_2,Butterworth),R_1=ev(R_1,Butterworth),R_2=ev(R_2,Butterworth))));

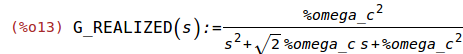
(%i14) ratsimp(ev(abs(G_REALIZED(s))^2,s=%i*%omega));

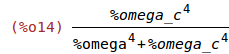
1.1 Bode Plots

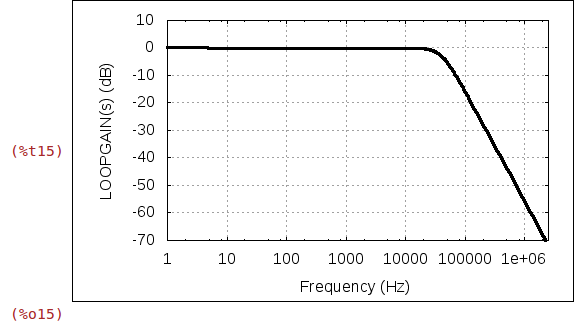
(%i15) wxplot2d(20*log(abs(ev(G_REALIZED(%i*2*%pi*f),%omega_c=2*%pi*40000)))/log(10),
[f,1,2.5e6],
[logx],
[xlabel,"Frequency (Hz)"],
[ylabel,"LOOPGAIN(s) (dB)"],
[style,[lines,3,11]],
[gnuplot_preamble,"set grid"]);

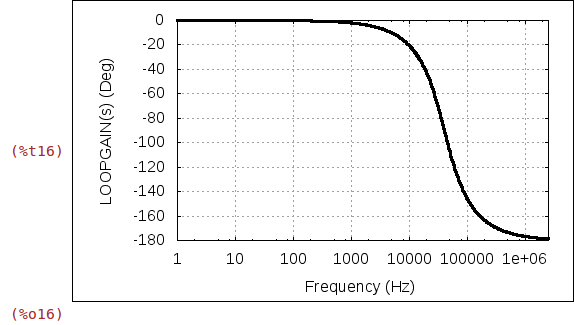
(%i16) wxplot2d(180/%pi*ArgSymbolic(ev(G_REALIZED(%i*2*%pi*f),%omega_c=2*%pi*40000)),
[f,1,2.5e6],
[logx],
[xlabel,"Frequency (Hz)"],
[ylabel,"LOOPGAIN(s) (Deg)"],
[style,[lines,3,11]],
[gnuplot_preamble,"set grid"]);