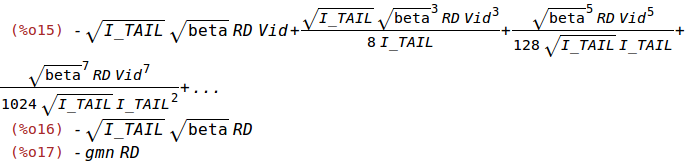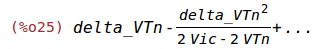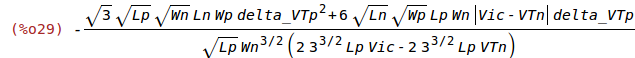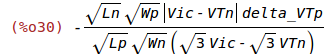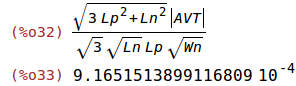Offset Analysis
(%i1)
declare([beta,beta_square,gmp,gmn,Lp,Ln,Vic,VTn,Wp,Wn,I_TAIL],[constant,real,scalar])$
assume(beta>0)$
assume(beta_square>0)$
assume(gmp>0)$
assume(gmn>0)$
assume(Lp>0)$
assume(Ln>0)$
assume(Vic>0)$
assume(VTn>0)$
assume(Wp>0)$
assume(Wn>0)$
assume(I_TAIL>0)$
1 Differential Pair with Resistive Load
1.1 No Mismatch
(%i13)
Solution:solve([
I_TAIL=I_1+I_2,
I_1=1/2*beta*(Vgs_1-VT)^2,
Vgs_1=Vg_1-Vs_12,
Vg_1=Vic+Vid/2,
I_2=1/2*beta*(Vgs_2-VT)^2,
Vgs_2=Vg_2-Vs_12,
Vg_2=Vic-Vid/2,
Vds_1=VDD-RD*I_1-Vs_12,
Vds_2=VDD-RD*I_2-Vs_12,
Vout=Vds_1-Vds_2],
[I_1,I_2,Vg_1,Vg_2,Vgs_1,Vgs_2,Vds_1,Vds_2,Vs_12,Vout]);
ev(Vout,Solution);

(%i15)
taylor(-(sqrt(beta)*Vid*sqrt(4*I_TAIL-beta*Vid^2)*RD)/2,Vid,0,7);
coeff(%,Vid,1);
ev(%,I_TAIL=gmn^2/beta);
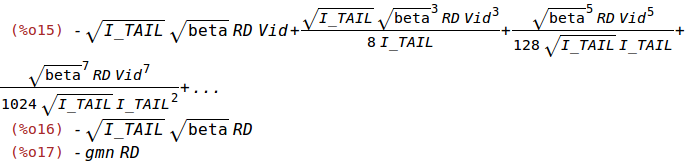
2 Differential Pair with Active Load
2.1 No Mismatch
(%i18)
Solution:solve([
I_TAIL=I_1+I_2,
I_1=1/2*betan*(Vgs_1-VTn)^2,
Vgs_1=Vg_1-Vs_12,
Vg_1=Vic+Vid/2,
I_2=1/2*betan*(Vgs_2-VTn)^2,
Vgs_2=Vg_2-Vs_12,
Vg_2=Vic-Vid/2,
I_3=-I_1,
Vgs_3=sqrt(2*(I_3)/betap)+VTp,
Vgs_4=Vgs_3,
I_4=1/2*betap*(Vgs_4-VTp)^2,
Iout=-(I_2+I_4)],
[Vgs_1,Vgs_2,Vgs_3,Vgs_4,Vg_1,Vg_2,Vs_12,Iout,I_1,I_2,I_3,I_4]);

(%i19)
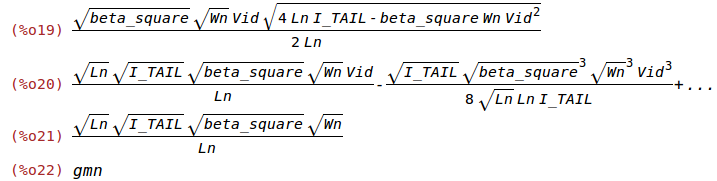
ratsimp(ev((sqrt(betan)*Vid*sqrt(4*I_TAIL-betan*Vid^2))/2,
betan=beta_square*Wn/Ln));
taylor(%,Vid,0,3);
coeff(%,Vid,1);
Gm:ev(%,I_TAIL=gmn^2/(beta_square*Wn/Ln));
2.2 With mismatch
(%i23)
Solution:solve([
I_TAIL=I_1+I_2,
I_1=1/2*betan*(Vgs_1-VTn)^2,
Vgs_1=Vg_1-Vs_12,
Vg_1=Vic,
I_2=1/2*betan*(Vgs_2-(VTn+delta_VTn))^2,
Vgs_2=Vg_2-Vs_12,
Vg_2=Vic,
I_3=-I_1,
Vgs_3=sqrt(2*(I_3)/betap)+VTp,
Vgs_4=Vgs_3,
I_4=1/2*betap*(Vgs_4-VTp)^2,
Iout=-(I_2+I_4)],
[Vgs_1,Vgs_2,Vgs_3,Vgs_4,Vg_1,Vg_2,Vs_12,Iout,I_1,I_2,I_3,I_4]);

(%i24)
IOSout:ev((sqrt(betan)*delta_VTn*sqrt(4*I_TAIL-betan*delta_VTn^2))/2,
betan=beta_square*Wn/Ln,
I_TAIL=1/2*beta_square*Wn/Ln*(Vic-VTn)^2+1/2*beta_square*Wn/Ln*(Vic-(VTn+delta_VTn))^2);

(%i25)
VOSin:taylor(ev(IOSout/(beta_square*Wn/Ln*(Vic-VTn))),delta_VTn,0,2);
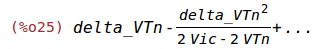
(%i26)
VOSin:taylor(ev(IOSout/(beta_square*Wn/Ln*(Vic-VTn))),delta_VTn,0,1);

(%i27)
Solution:solve([
I_TAIL=I_1+I_2,
I_1=1/2*betan*(Vgs_1-VTn)^2,
Vgs_1=Vg_1-Vs_12,
Vg_1=Vic,
I_2=1/2*betan*(Vgs_2-VTn)^2,
Vgs_2=Vg_2-Vs_12,
Vg_2=Vic,
I_3=-I_1,
Vgs_3=sqrt(2*(I_3)/betap)+VTp,
Vgs_4=Vgs_3,
I_4=1/2*betap*(Vgs_4-(VTp+delta_VTp))^2,
Iout=-(I_2+I_4)],
[Vgs_1,Vgs_2,Vgs_3,Vgs_4,Vg_1,Vg_2,Vs_12,Iout,I_1,I_2,I_3,I_4]);

(%i28)
IOSout:ratsimp(ev(-(betap*delta_VTp^2+2*sqrt(I_TAIL)*sqrt(betap)*delta_VTp)/2,
betap=1/3*beta_square*Wp/Lp,
I_TAIL=beta_square*Wn/Ln*(Vic-VTn)^2));

(%i29)
VOSin:ratsimp(taylor(ev(IOSout/(beta_square*Wn/Ln*(Vic-VTn))),delta_VTp,0,2));
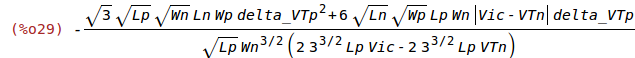
(%i30)
VOSin:ratsimp(taylor(ev(IOSout/(beta_square*Wn/Ln*(Vic-VTn))),delta_VTp,0,1));
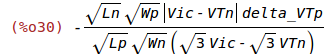
(%i31)
VOSin_total:sqrt(delta_VTn^2+(-(sqrt(Ln)*sqrt(Wp)*delta_VTp)/(sqrt(Lp)*sqrt(Wn)*sqrt(3)))^2);

(%i32)
VOSin:ratsimp(ev(VOSin_total,
delta_VTp=AVT/sqrt(Wp*Lp),
delta_VTn=AVT/sqrt(Wn*Ln)));
float(ev(%,Wn=50e-6,Ln=2e-6,Wp=36e-6,Lp=1e-6,AVT=6e-9));
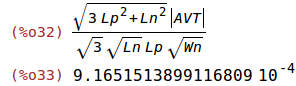
Created with wxMaxima.