Amplitude-Frequency Hysteresis in Flexural-Mode Vibrating RF MEMS Resonators

References:
- Ch. 28 (Anharmonic Oscillations) and Ch. 29 (Resonance in Non-Linear Oscillations) in Mechanics by L. D. Landau and E. M. Lifshitz, Butterworth-Heinemann, January 15, 1976
- http://www.kaajakari.net/~ville/research/tutorials/nonlinear_resonators_tutorial.pdf

(%i1) declare([%kappa,%mu,%nu,%rho,%omega,C_0,E,g_0,k_1,k_3,l,t,V_S,w],[constant,real,scalar])$
assume(%kappa>0)$
assume(%mu>0)$
assume(%nu>0)$
assume(%rho>0)$
assume(%omega>0)$
assume(C_0>0)$
assume(E>0)$
assume(g_0>0)$
assume(k_1>0)$
assume(k_3>0)$
assume(l>0)$
assume(t>0)$
assume(V_S>0)$
assume(w>0)$

1 Amplitude-Frequency Coefficient

(%i16) %kappa:3*k3eff/(8*k1eff)*%omega-5*k2eff^2/(12*k1eff^2)*%omega;

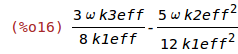
Result

(See: Eq. 28.13 in Mechanics by L. D. Landau and E. M. Lifshitz, Butterworth-Heinemann, January 15, 1976)

1.1 One-Sided Actuation

(%i17) Fe:taylor(1/2*(C_0*g_0)/(g_0-z)^2*(V_S+v_in)^2,z,0,9);

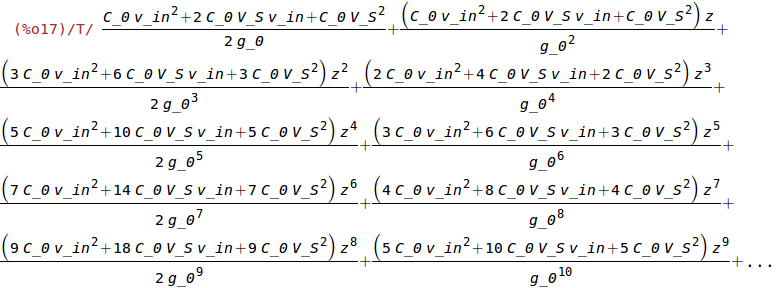
Result

(%i18) %kappa_k1:ev(%kappa, k1eff=k_1-V_S^2*C_0/g_0^2, k2eff=-3/2*V_S^2*C_0/g_0^3, k3eff=k_3-2*V_S^2*C_0/g_0^4);
tex(%)$

Result

(%i20) ratsimp(%kappa_k1);

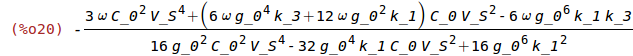
Result

1.2 Two-Sided Actuation

(%i21) Fe:taylor(1/2*(C_0*g_0)/(g_0-z)^2*(V_S+v_in)^2-1/2*(C_0*g_0)/(g_0+z)^2*V_S^2,z,0,9);

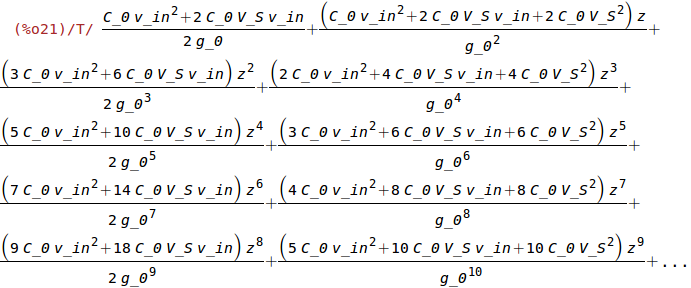
Result

(%i22) %kappa_k1:ev(%kappa, k1eff=k_1-2*V_S^2*C_0/g_0^2, k2eff=0, k3eff=k_3-4*V_S^2*C_0/g_0^4);
tex(%)$

Result

(%i24) ratsimp(%kappa_k1);

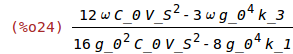
Result

Rewriting as a function of omega, eliminating l

(%i25) k1:(32*E*t^3*w)/l^3*(27/49);

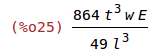
Result

(%i26) m:0.396*%rho*l*t*w;

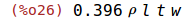
Result

(%i27) sqrt(k1/m);

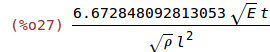
Result

(%i28) l_omega:sqrt(6.672848092813053*t*sqrt(E/%rho)/omega);

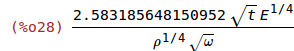
Result

(%i29) k1_omega:(32*E*t^3*w)/l_omega^3*(27/49);

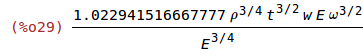
Result

2 Critical Displacement

(%i30) zc:ratsimp(sqrt(4*%omega)/(sqrt(3*sqrt(3)*Q*abs(%kappa_k1))));

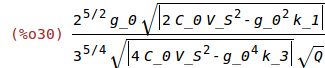
Result

(See: Eq. 29.7 in Mechanics by L. D. Landau and E. M. Lifshitz, Butterworth-Heinemann, January 15, 1976)

(%i31) float(ev(zc,C_0=1.85e-16,g_0=0.33e-6,k_1=1.505e3,k_3=-6.2e15,Q=6.76e3,V_S=70));

Result

(%i32) float(sqrt(1.51e3/2.28e-13));

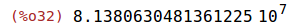
Result

3 Maximum Average Energy Storage (Kinetic and Potential (Elastic))

(%i33) Emax_k:ratsimp(1/2*(k_1-2*V_S^2*C_0/g_0^2)*zc^2);

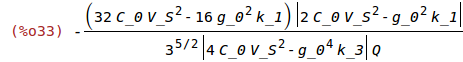
Result

Rewriting as a function of omega, eliminating l

(%i34) Emax_k_l:ratsimp(ev(Emax_k,k_1=k1_omega));

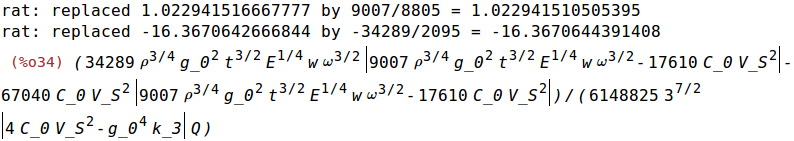
Result

4 Mechanical Q Factor

(%i35) Q:(sqrt(E*%rho)*t^2*g_0^3)/(%mu*(w*l/2)^2);

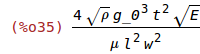
Result

(%i36) Q_l:(sqrt(E*%rho)*t^2*g_0^3)/(%mu*(w*l_omega/2)^2);

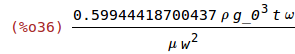
Result

Q varies with 1/w^2 if %omega is held fixed. Q goes up is w is scaled.

5 Dissipated Power

(%i37) P_diss:ratsimp(ev(%omega*Emax_k_l/Q,Q:Q_l));

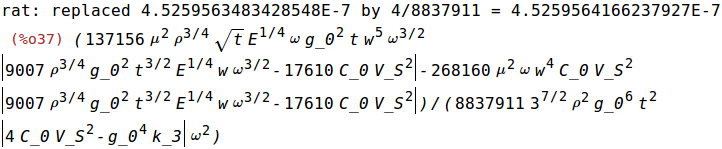
Result

P_diss varies with w^6 if %omega is held fixed. P_diss goes down if w is scaled.

Created with wxMaxima.